Damenproblem

Einführung

Die Dame, englisch Queen, ist die stärkste Figur im Schach. Sie kann sich sowohl diagonal wie ein Läufer als auch gerade wie ein Turm in jede Richtung auf dem Brett beliebig weit bewegen. Deshalb besitzt normalerweise jeder Spieler auch nur eine Dame. Allerdings kann ein Bauer, der auf die Grundlinie des Gegners bewegt wurde, in eine beliebige Figur umgetauscht werden. Man könnte also bei der rechts abgebildeten (und theoretisch sogar möglichen) Stellung von einem Damen-Problem für Schwarz sprechen. Doch es lohnt sich auch abseits des Schachspiels über die Zugmöglichkeiten und Kombinationen von Figuren nachzudenken. Die sich ergebenden Fragestellungen sind zumeist mathematischer Natur und haben viel mit Geometrie und Logik zu tun. Und mithilfe von Computern lassen sich tausende Lösungen pro Sekunde nachrechnen und die theoretischen Beweise praktisch überprüfen.

Das Damenproblem ist ein echter Klassiker unter Schachliebhabern. Man nehme acht Damen beliebiger Farbe und ein rechteckiges Schachbrett: Ist es möglich, die acht Damen auf dem 8x8 Brett so zu positionieren, dass keine die andere sehen/schlagen kann? Es dürfen also keine zwei Damen auf derselben Reihe, Spalte oder Diagonale stehen. Die Antwort ist: Ja, es ist möglich. Mit ein wenig Fantasie und etwas Geduld kommt man bald auf eine Lösung, zum Beispiel indem man bei A1 (ein Feld über der linken unteren Ecke) startet und jeweils um zwei Felder versetzt pro Reihe eine neue Dame hinzufügt. Gegen Ende wird es etwas kniffliger, aber es ist schaffbar. Nun fragt der Mathematiker: Ist die gefundene Lösung die einzig mögliche? Und wie verhält es sich im Allgemeinen, also wie viele Lösungen gibt es jeweils für n Damen auf einem n mal n Brett? Dazu haben sich schon früh verschiedene Menschen Gedanken gemacht, doch erst seit kurzem ist es auch möglich, mithilfe von Computern auch für große n (Rekord liegt derzeit bei 27) alle Lösungen auszurechnen. Vorausgesetzt man hat einen entsprechend effizienten Algorithmus.

Problemstellung

Mathematisch betrachtet lässt sich ein Schachbrett ungeachtet der schwarz-weiß-Färbung als eine Art Koordinatensystem darstellen. Ich beginne hier bei der Zählung mit 1, es ist aber ebenso möglich das erste Feld mit 0:0 zu benennen. In jedem Fall gilt: Eine Dame kann die andere schlagen, falls …

• a) x₁ = x₂
• b) y₁ = y₂ oder
• c) |x₁-x₂| = |y₁-y₂|

Eine Stellung gilt als valide, wenn diese drei Möglichkeiten für alle paarweisen Kombinationen ausgeschlossen sind. Klingt simpel, jedoch gibt es bereits beim herkömmlichen Schachbrett fast 248 Möglichkeiten, acht Damen aufzustellen. Das macht rund 263 notwendige Vergleiche! Für größere Bretter braucht es also zwingend eine Strategie, diejenigen Kombinationen möglichst früh herauszufiltern, die zu keiner Lösung führen können. Das kann dynamisch oder auch rekursiv geschehen. Zuletzt muss man sich außerdem entscheiden, ob man seine Lösungen in einer Variable speichern oder direkt mit der Berechnung ausgeben möchte. Während das Speichern viel Arbeitsspeicher verbraucht, können Ausgaben nämlich die Berechnung blockieren und unnötig viel Zeit kosten. Auf der anderen Seite muss sichergestellt werden, dass keine Lösungen übersehen werden, dass das Programm auf jede Eingabe terminiert und dass nur solche Lösungen ausgegeben werden, die tatsächlich n Damen enthalten.

Ansatz

Zuerst hatte ich die Idee für einen Divide-and-Conquer-Algorithmus. Dabei wird das Schachbrett so lange in einer Richtung halbiert, bis man eine einzelne Spalte mit einer Dame erhält. Hier ist jede mögliche Position der Dame eine Lösung, sprich A0, A1, A2, A3, A4, A5, A6, A7. Fügt man eine Spalte an, sind alle paarweisen Kombinationen der zwei Damen auf ihrer einzelnen Spalte eine Lösung abzüglich der Stellungen, in denen sich die Damen schlagen können, sprich (A0,B2), (A0,B3), (A0,B4), (A0,B5), (A0,B6), (A0,B7), (A1,B3), (A1,B4) … Allgemein müssen also die Teillösungen beim Zusammensetzen paarweise kombiniert und validiert werden. Von der Tiefe des Rekursionsbaums ist dies die eleganteste Lösung. Allerdings gibt es auf einem 4x8-Brett weit mehr Lösungen als auf einem 8x8-Brett. Dazu entstehen beim Zusammenfügen je quadratisch viele neue Kandidaten, die überprüft werden müssen. Das Ergebnis ist ein Haufen unnötiger Vergleiche.

Effektiver ist es, mit einer Spalte zu beginnen und in jedem Schritt nur eine weitere Spalte anzufügen. Es ergibt sich ein dynamischer Algorithmus. Das Prinzip ist das gleiche wie vorher, bloß wird stets ein Brett der Breite t mit einer einzelnen Spalte der Länge n kombiniert. So wächst die Anzahl der Zwischenlösungen in jedem Schritt maximal um den Faktor n. Das Ganze kann als einfache for-Schleife bottom-up oder auch rekursiv top-down implementiert.

Lösung

Der Algorithmus funktioniert folgendermaßen: Es wird eine Schleife n-mal durchlaufen. In jedem Schleifendurchlauf t wird eine Liste der Länge n erzeugt, wobei jedes Element den x-Wert t und den y-Wert i erhält, wobei i der jeweilige Platz in der Liste ist. Nun wird für jedes Element der neuen Liste überprüft, mit welchen vorangegangen Lösungen es kompatibel ist. Alle invaliden Kombinationen werden verworfen. Ist die Tiefe t=n erreicht, werden die Lösungen zeilenweise auf dem Bildschirm ausgegeben.

Bei der Implementierung habe ich mich für die Programmiersprache Java entschieden. Dabei habe ich je eine Klasse für das Schachbrett, die Damen und die Problemlösung erstellt. Die Damen erhalten als Attribute stets eine x und eine y-Koordinate. Das Brett erhält eine Reihen- und eine Spaltenanzahl sowie zwei Zähler. Die rekursive Lösungsfunktion erhält in jedem Aufruf eine Liste der vorangegangenen Lösungen und eine Zählerangabe (Tiefe bezieht sich hier auf den Rekursionsbaum). Der Zähler ersetzt den Iterator der for-Schleife.

Als Variation der vorangegangenen Beschreibung werden die neuen Damen nicht direkt als Liste, sondern einzeln für jede neue Kombination erzeugt. Das spart eine weitere Abfrage. Die neue Kombination ist genau dann valide, wenn für alle Damen aus der alten Lösungen mit der neuen Damen gilt, dass sie sich nicht schlagen können. Die Funktion valid2 fragt dabei nacheinander die obigen Kriterien ab. Sind alle paarweisen Vergleiche valide, wird eine neue Liste erzeugt, der alle Damen hinzugefügt werden. Dies ist notwendig, weil die alte Liste noch für andere Kombinationen benötigt wird. Im letzten Schritt geschieht ein rekursiver Aufruf mit der neuen Liste und der zuvor inkrementierten Zählervariable.

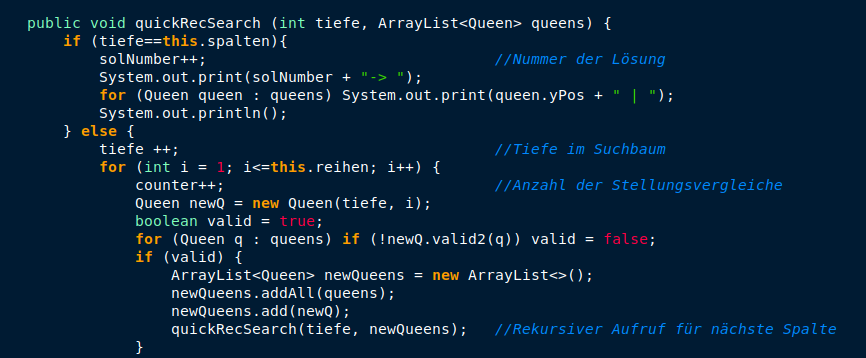
Die Ausgabe erfolgt, indem jede Lösung, welche alle Vergleiche übersteht, direkt mittels println() ausgegeben wird. Da mit der Anzahl der Damen die Menge der Lösungen exponentiell steigt, verzichte ich aus Performancegründen in diesem Beispiel auf eine Zwischenspeicherung. Warum dies ab einer bestimmten Größe sogar zwingend erforderlich ist, erkennt man, wenn man die Lösungen zusätzlich mittels FileWriter in einer Textdatei abspeichert. Für n=17 ist diese Datei am Ende mehrere Gigabyte groß. Aus eigener Erfahrung kann ich sagen, dass der Arbeitsspeicher da (sehr) schnell an seine Grenzen kommt.

Korrektheit

Zunächst kann man recht einfach zeigen, dass der Algorithmus für jedes endliche n terminiert: Die Lösungsfunktion wird mit t=0 gestartet und t in jedem rekursiven Aufruf um eins erhöht. Ist t>=n, finden keine weiteren rekursiven Aufrufe statt. Alle anderen Funktionen enthalten lediglich if-Abfragen und for-Schleifen, die naturgemäß auf jede Eingabe terminieren.

Im zweiten Schritt lässt sich ausschließen, dass Lösungen ausgegeben werden, für die obige Kriterien verletzt werden. Dafür betrachtet man die for-Schleife in Zeile 47. Falls die Liste queens eine valide Zwischenlösung darstellt und jeder paarweise Vergleich mit der neu gebildeten Dame valide ist, so ist es per Definition auch die neu gebildete Liste. Und da jede Zwischenlösung nach demselben Muster gebildet wurde und die Basislösung – eine einzelne Dame in einer Spalte – in jedem Fall valide ist, kann ausgeschlossen werden, dass ausgegebene Lösungen die obigen Kriterien verletzen.

Und zu guter Letzt die Vollständigkeit: Die for-Schleife in Zeile 43 hat für quadratische Bretter genau n Durchläufe und in jedem Durchlauf wird eine neue Dame gebildet mit der jeweiligen Tiefe als x und i als y-Wert. Bei n rekursiven Aufrufen werden also insgesamt n² viele Damen erzeugt und wie zuvor beschrieben jede mit jeder anderen Dame aus einer anderen Spalte verglichen. Dass tatsächlich deutlich weniger Vergleiche passieren, liegt daran, dass der Großteil implizit stattfindet. Anders gesagt werden keine Zwischenlösungen mehr in Betracht gezogen, in denen bereits ein Fehler gefunden wurde. Diese Vereinfachung ist legal und darüber hinaus notwendig, da die Lösungsfunktion vorangegangene Zwischenlösungen nicht mehr in Frage stellt und auch nicht verändert. Da aber sämtliche validen Zwischenlösungen weitergegeben werden und jede Lösung zwingend n Damen enthalten muss, kann keine Lösung übersehen werden und die Ausgabe ist vollständig.

Laufzeit

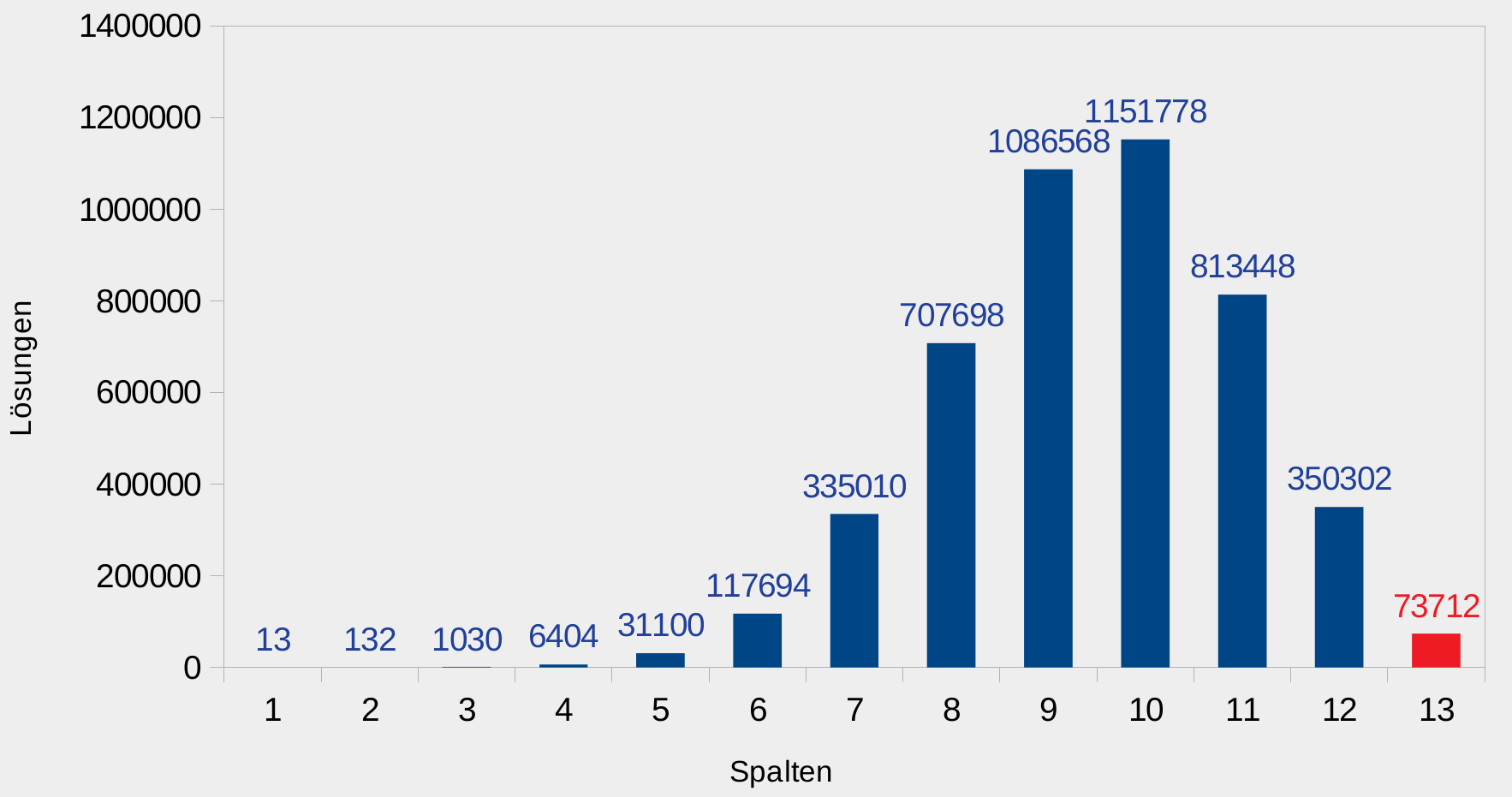Interessanterweise ist gar nicht bekannt, in welcher Größenordnung die Anzahl der Lösungen mit der Seitenlänge wächst. Für n=2 und n=6 reduziert sich sogar die Anzahl im Vergleich zum Vorgänger. Es lässt sich lediglich zeigen, dass ab einer bestimmten Größe immer mindestens eine Lösung existiert und im schlimmsten Fall maximal n! Lösungen. Doch selbst wenn die Anzahl der endgültigen Lösungen in etwa bekannt wäre, genügte dies nicht einer Laufzeitanalyse des hier vorgestellten Algorithmus. Dieses Problem ist viel komplexer. Dazu habe ich die nebenstehende Grafik erstellt.

Zu sehen ist die Anzahl der Zwischenlösungen bei einem 13x13 Brett. Der Algorithmus beginnt mit einer einzelnen Spalte mit einer Dame und kommt auf 13 Lösungen, da jedes Feld eine Lösung ist. Fügt man eine Spalte hinzu, wächst die Anzahl auf 132, da jede Kombination zweier Damen eine Lösung ist bis auf diejenigen, die durch die valid2-Funktion aussortiert werden. Auch bei drei Spalten wächst die Lösungsanzahl wie erwartet grob um den Faktor n, doch schon bei vier Spalten beträgt der Faktor nur noch n/2. Der Algorithmus hat eine Stufe erreicht, ab der er fleißig aussortieren kann, da der Platz in den Spalten für die Damen mit jeder neuen Dame enger wird und immer weniger valide Lösungen gefunden werden. Das Maximum der Zwischenlösungen wird mit mehr als 1,1 Millionen bei zehn Spalten erreicht. Danach werden, bildlich gesprochen, selbst starke Äste im Rekursionsbaum abgesägt, da für bestimmte Anfangskonstellationen keine Dame in der neuen Spalte eine valide Kombination ermöglicht. Millionen Zwischenlösungen wurden quasi umsonst ausgerechnet. Es ist leicht an dem Diagramm abzulesen, dass nicht die Anzahl der endgültigen Lösungen die Laufzeit unseres Programms bestimmt, sondern vielmehr die Anzahl der zu berechnenden Zwischenlösungen.

Auf meinem Laptop braucht das Programm für die Berechnung der 73.712 Lösungen ohne Ausgabe nur 3,5 Sekunden, bei n=16 kann man sich dafür bereits in der Zwischenzeit einen Kaffee kochen. Wäre es möglich, diejenigen Zwischenlösungen frühzeitig auszusortieren, welche in keiner Kombination mit einer neuen Dame zu einer Lösung führen können, bedeutete das einen Zeitgewinn um einen Faktor 10 oder mehr. Denkbar wäre beispielsweise, mit einem 1x1 Brett zu beginnen und immer abwechselnd eine Reihe ohne neue Dame und eine Spalte mit neuer Dame hinzuzufügen (würde man auch bei neuen Reihen Damen hinzufügen, käme man am Ende auf n² Damen statt auf n). Mit diesem System würde die Laufzeit lediglich mit der Anzahl der Lösungen auf quadratischen Brettern wachsen. Leider ist das aber nicht ohne Weiteres möglich. Während man bei der Zunahme einer neuen Spalte ganz genau die neuen Lösungen aus den alten definieren kann, scheinen die Lösungen nach Zunahme einer neuen Reihe keinen Bezug mehr zu den vorherigen Lösungen zu besitzen.

Es ist unbefriedigend, die Laufzeitanalyse lediglich für die beiden Fälle aufstellen zu können, bei denen entweder genau eine Lösung existiert oder jede Kombination eine Lösung ist (was ebenso unrealistisch ist). Im Best Case bedeutet das also lediglich O(n³) Vergleiche, da jeder Funktionsaufruf durch die zwei verschachtelten for-Schleifen in Z. 43 und Z. 47 n² Vergleiche erzeugt und stets nur ein rekursiver Aufruf geschieht. Ein Vergleich entspricht dabei einem Aufruf der valid2-Funktion. Im Worst Case geschehen dagegen pro Funktionsaufruf von quickRecSearch n weitere rekursive Aufrufe, wodurch man auf eine Zahl von n + n² + n³ + … + nⁿ Zwischenlösungen kommt. Mit maximal n Vergleichen je neuer Dame liegt die Laufzeit von QuickRecChess im Worst Case damit in O(nⁿ⁺¹). Für den Average Case bräuchte man jetzt eine Wahrscheinlichkeitsfunktion für die Verteilung der Zwischenlösungen, die ich nicht habe. Meinen Messergebnissen bis n=17 zufolge könnte die Laufzeit in O(n^n/2) liegen. Jedoch ist völlig unklar, wie sich die Laufzeit für große n verhalten würde, gäbe es entsprechende Rechenkapazitäten.

QuickRecChess.java