Palindrome

Einführung

Sprache hat viel mehr mit Mathematik und Symmetrie zu tun, als man zunächst denkt. Nicht umsonst programmiert man Computer heutzutage mit sogenannten Hochsprachen. Ein alltägliches Beispiel dagegen liefert uns dagegen der Aufbau unserer Schrift in Buchstaben und Wörtern. In der Lyrik macht man sich diese Bildhaftigkeit zu Nutze und erzeugt Alliterationen, Metaphern, Allegorien und Onomatopoesien. Mathematisch noch interessanter sind Anagramme, eine Form der Permutation, bei welcher neue Wörter entstehen. Aus dem Wort REGALLAGER wird LAGERREGAL. Versucht man allerdings, diese beiden Wörter vertikal zu spiegeln, fällt einem auf, dass sie noch etwas gemeinsam haben.

Problemstellung

Ein Palindrom ist ein Wort, sprich eine Aneinanderreihung von Buchstaben, welches von vorne wie von hinten gelesen dasselbe ergibt. Ein Beispiel ist das Wort EBBE. Da nun nur sehr wenige Wörter als ganze diese Eigenschaft besitzen, stellt sich nun die Frage, wie oft man ein beliebiges Wort mindestens zerteilen muss, um eine Zerlegung in Palindrome zu erhalten. Während die Palindromzerlegung (PZ) häufig nicht eindeutig ist – das Wort RETTEN lässt sich ebenso in R|E|TT|E|N wie in R|ETTE|N zerlegen, beschreibt die Palindromlänge pl(w) die minimale Anzahl Palindrome von sämtlichen möglichen Palindromzerlegungen. Daher ist pl(RETTEN) = 3. Ein Palindrom hat stets die Länge eins.

Die maximale Anzahl Zerlegungen zu finden ist simpel, sie wird durch die Trennung in einzelne Buchstaben erreicht, da jeder Buchstabe gleichzeitig ein Wort und damit ein Palindrom ist. Das Problem ist also, für ein beliebiges Wort die minimale Anzahl Zerlegungen zu finden, die Palindromlänge.

Ansatz

Gegeben ist ein beliebiges Wort w. Ist w ein Palindrom, ist pl(w) = 1 und wir sind fertig. Ist w dagegen kein Palindrom, suchen wir alle möglichen PZ von w und berechnen davon das Minimum. Hierfür zerteilen wir w in die beiden Teilwörter w₁ und w₂. Kennen wir pl(w₁) und pl(w₂), so bestimmen wir w₁ und w₂ genau so, dass pl(w₁) + pl(w₁) minimal ist. Dies ist also ein rekursiver Ansatz – wir überprüfen für jedes Teilwort, ob es ein Palindrom ist, andernfalls zerteilen wir es wieder in zwei Teilwörter. Diese Zerteilung geschieht so lange, bis alle Teilwörter Palindrome oder einzelne Buchstaben sind. Nun können wir die Palindromlängen der übergeordneten Teilwörter berechnen, bis wir schließlich die Palindromlänge des gesamten Wortes erhalten. Um effektiv auf die errechneten Zwischenergebnisse zurückgreifen zu können, speichern wir diese in einer quadtratischen Matrix ab, die leicht als Array realisiert werden kann.

Lösung

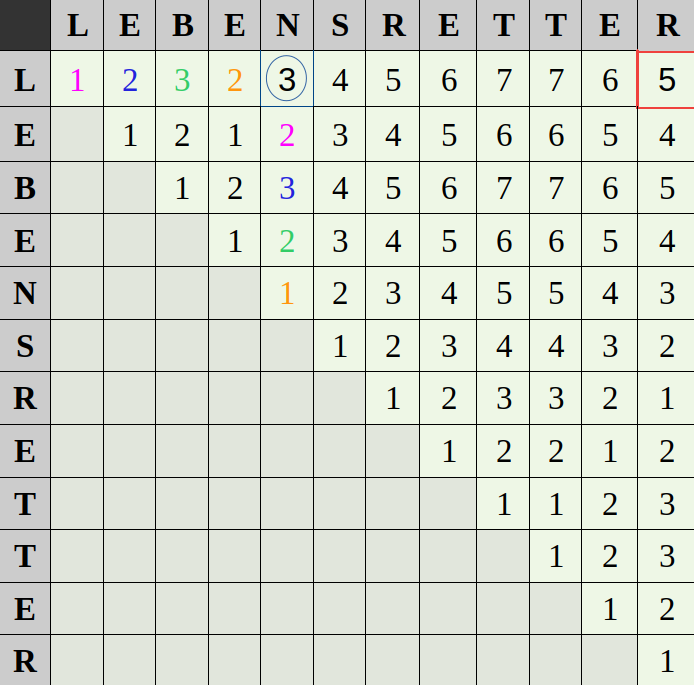
Zunächst legen wir fest, dass ein Wort genau dann ein Palindrom ist, wenn das Wort als Liste von Buchstaben gleich der Liste von Buchstaben in umgekehrter Reihenfolge ist. Weiter legen wir fest, dass m_i,j die Zelle in der i-ten Zeile und j-ten Spalte ist und dass w_i,j das Teilwort vom i-ten bis zum j-ten Buchstaben von w beschreibt. Darauf aufbauend sieht unser Algorithmus folgendermaßen aus:

1. Erstelle eine n × n Matrix M mit n gleich der Länge des Wortes w. (Im Beispiel rechts wäre n = 12)
2. Definiere den Inhalt jeder Zelle als m_i,j = 1, wenn w_i,j ein Palindrom ist und m_i,j = min(m_i,i+k + m_i+k+1,j mit k = 0...j-i-1), wenn w_i,j kein Palindrom ist. Speichere dabei alle Zwischenergebnisse in M ab, sodass jede Zelle höchstens einmal berechnet werden muss.
3. Gib den Inhalt von m_1,n als pl(w) aus.

Ausformuliert bedeutet der zweite Punkt, dass wir alle möglichen Teilworte von w bestimmen und deren Palindromlänge berechnen. Dabei ist die Palindromlänge eines Teilworts die Summe der Palindromlängen bei optimaler Kombination der untergeordneten Teilwörter. Im Beispiel rechts müssen für das Teilwort LEBEN die Summen 1+2, 2+3, 3+2 und 2+1 berechnet werden. Das Minimum davon ist 3, also ist pl(LEBEN) = 3.

Korrektheit

Die Palindromlänge ist gegeben durch die Anzahl enthaltener Palindrome bei optimaler Zerlegung. Hierfür müssen alle Teilwörter von w mindestens einmal betrachtet werden. Dies geschieht im Algorithmus durch die zwei Dimensionen der Matrix. m1,n ist entweder 1 oder das Minimum aus m_i,i+k + m_i+k+1,j mit k = 0...j-i-1. Dabei stellt das k sicher, dass alle enthaltenen Zerlegungen in zwei Teilwörter betrachtet werden. Und da in jeden Rekursionsschritt das Teilwort um mindestens einen Buchstaben gekürzt wird und bei einer Länge von 1 die Palindromlänge auf jeden Fall definiert ist, terminiert der Algorithmus und gibt folglich die korrekte Palindromlänge des Wortes w_1,n = w aus.

Laufzeit

Ist keine Palindromlänge eines enthaltenen Teilworts bekannt, so müssen in jedem Fall (n²+n)/2 Matrixelemente berechnet werden. Für jedes Element müssen dabei maximal (n-1) Additionen durchgeführt werden. Bei konstanter Zugriffszeit auf die Matrix durch die Verwendung eines Arrays läuft jede einzelne Addition in konstanter Zeit. Insgesamt ergibt sich so eine Laufzeit von ((n²+n)/2)*(n-1)*c ∈ O(n³). Also ist die Laufzeit kubisch zur Länge des eingegebenen Wortes.

Palindromlaenge.py