O-Notation

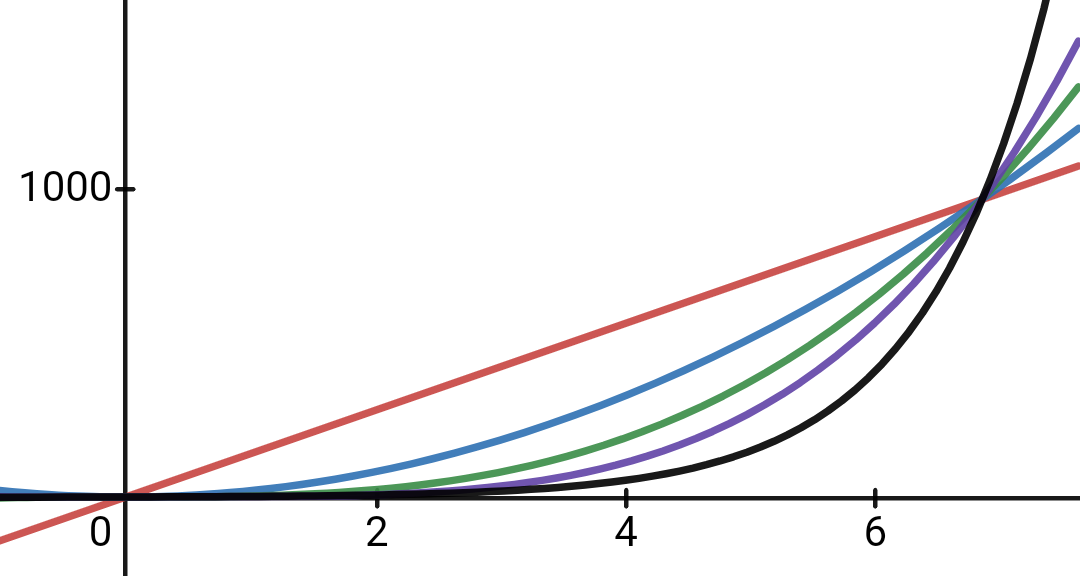
Einer der wichtigsten Eigen­schaften eines Algo­rithmus ist seine Laufzeit bei großen Eingaben. Fast jedes mathe­matische Problem lässt sich lösen, indem man sämtliche Möglich­keiten systematisch ausprobiert. Betrachten wir hierzu wieder das Sortieren. Eine Folge von Zahlen ist sortiert, wenn der Nach­folger jeden Gliedes größer ist als sein Vorgänger. Bei 10 oder 20 Zahlen spricht nichts dagegen, einfach sämt­liche Reihen­folge-Kombi­nationen aufzuschreiben und danach zu schauen, welche Kombi­nation sortiert ist. Problem gelöst. Dass dieser Ansatz sehr ineffizient ist, leuchtet jedem ein, aber was soll’s? Ein moderner Prozessor rechnet im Gigaherz-Bereich, führt also mehrere Milliarden Befehle pro Sekunde aus.

Allerdings sortiert ein Computer nicht nur dann, wenn wir zum Spaß eine Folge von Zahlen eintippen und auf Enter drücken. Ohne dass der Benutzer etwas davon mitkriegt, werden jede Minute Unmengen von Daten sortiert, damit später bequem darauf zugegriffen werden kann. Und da geht es nicht um eine handvoll Werte, sondern um viele Milliarden. Nun hängt es von der Güte des Algorithmus ab, wie schnell sich der Ladebalken auf dem Bildschirm vorwärts bewegt, wenn wir einen USB-Stick einstecken oder eine Netflix-Serie laden. Und bereits eine marginale Erhöhung der Datenmenge kann die Laufzeit von manchen Algorithmen explodieren lassen. Das Sortierproblem ist da noch recht zahm. Eine Verdopplung der Eingabe führt bei guter Implementierung zu weniger als einer Vervierfachung der Laufzeit. Beim Problem des Handelsreisenden dagegen kann sich die Laufzeit vertausendfachen, obwohl die Eingabe nur um einen Bruchteil erhöht wurde. Und es werden zwangsläufig immer mehr Daten. Allein eine https-Seite wie diese hier aufzurufen verlangt ihrem Computer Höchstleistungen ab. Grafik, Kommunikation, Verschlüsselung, Speicher – je mehr Ansprüche wir an unser digitales Erlebnis stellen, desto mehr Daten fallen an und desto schneller müssen Computer werden, ohne dass wir sie vor Ungeduld wüst beschimpfen.

Sie merken: Es geht in der Informatik gar nicht darum, eine feste Zeit festzulegen, in der ein Programm durchgelaufen sein muss. Es geht darum, dass man noch in der Zukunft mit dem Programm weiterarbeiten will, wenn die Menge an zu verarbeitenden Daten vielleicht um 100, 200 oder 1000% gewachsen ist.

Damit hätten wir eine Motivation geschaffen, uns näher mit der Laufzeitanalyse auseinander zu setzen. Nun stellt sich aber die Frage, wie wir eine Eigenschaft mathematisch beschreiben und im besten Fall vergleichen können, die unmittelbar von der jeweiligen Eingabe abhängt und zudem in einer Größenordnung jenseits unserer Vorstellungskraft liegt. Wir können staunen, wenn wir hören, dass ein Hacker ein 10-stelliges Passwort in unter 100 Jahren knacken kann, aber dem Entwickler von Sicherheits-Software hilft das wenig. Auch spielt es für den ersten Entwurf keine Rolle, ob ein Programm 10% schneller oder langsamer ist, da solche konstanten Faktoren später immer noch optimiert werden können. Und weil wir nicht wissen, wie viele Daten wir später noch verarbeiten wollen, betrachten wir die Laufzeit für beliebig große Eingaben.

1. Konstante Faktoren sind nicht von Interesse
2. Laufzeit abhängig von Eingabegröße n

Die O-Notation ist eine sehr elegante Art, mathematische Funktionen nach ihrem asymptotischen Wachstum zusammenzufassen. Asymptotisch bedeutet hier, dass wir keine obere Grenze für die Eingabe festlegen.

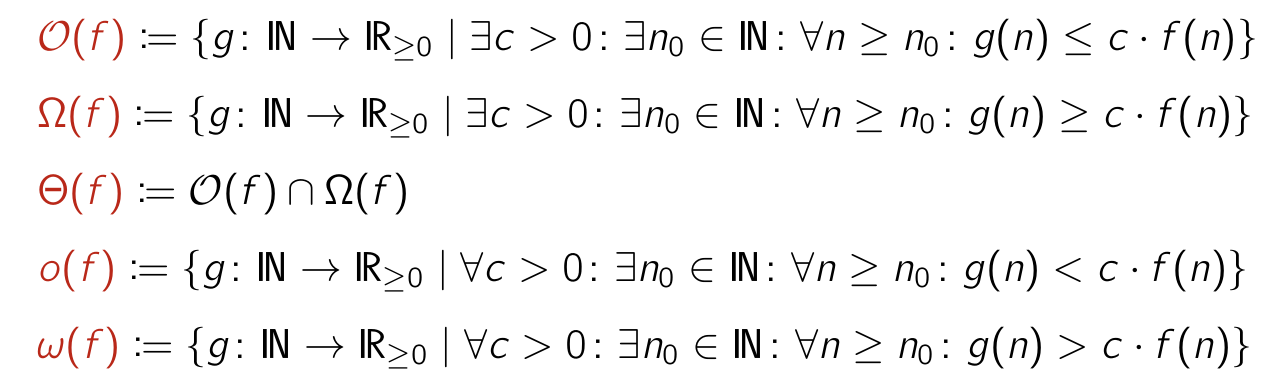
keine